17岁高中生一战封神！推翻40年数学猜想，起因竟是一道选做题

编辑：KingHZ

【新智元导读】17岁女孩Hannah Cairo，用反例颠覆数学界数十年的信仰！这一困扰了学者几十年的问题，居然被这位高中生「顺手解决」了？

40多年来，数学界相信Mizohata-Takeuchi猜想是对的。

虽然这从来没有被证明，但大家愿意相信它是对的：这样能自动推导出领域内多个重要结果。

这道题自然也难倒了17岁的Hannah Cairo。

连续几周，她冥思苦想，想要一个全新的解法。

经过几个月的努力，她渐渐明白为什么这个结论那么难以证明。

她意识到，或许可以反其道而行，构造出反例，彻底推翻猜想。失败了一次、两次、三次……终于，她成功了！

论文链接：https://arxiv.org/abs/2502.06137

她用到了多种工具，包括分形理论（fractals），并小心设计每一步推理，步步为营。

「我花了好一段时间，才让提问这道题的张瑞祥教授相信：我的方法是对的。」

张瑞祥现任加州大学伯克利分校数学系助理教授，2017年获普林斯顿大学数学博士学位，2012年毕业于北京大学数学系

她的想法确实没错——就这样，Cairo解决了所谓的Mizohata‑Takeuchi猜想 (Mizohata‑Takeuchi conjecture)。

该猜想最早在1980年代提出，调和分析 (harmonic analysis) 界研究了几十年。

学界普遍相信它是正确的——因为若它成立，就能自动推导出该领域中多个重要结果。

这下，全场震惊。年仅17岁、还没高中毕业的她，竟然解决了困扰数学界数十年的难题！

在张教授的指导下，她将于今年秋季进入马里兰大学，直接攻读博士学位。

她出生在巴哈马首都拿骚（Nassau），后来搬到美国，就读高中，但也在加州大学伯克利分校 (UC Berkeley) 上过课。

巴哈马是加勒比地区最富有的国家之一，地处美国佛罗里达礁岛群东南面，旅游业发达

她回忆道：「我给几位教授写邮件，介绍自己读过哪些相关书，并询问能否旁听。他们很多人都同意，包括张教授。」

有一天，张教授出了一个练习题：证明Mizohata‑Takeuchi猜想某个特殊但更简单的情形。作为选做题，他还给出了原始猜想。

自那时起，Cairo就完全被它吸引住了。

40难未解之谜

Mizohata‑Takeuchi猜想

Mizohata‑Takeuchi猜想属于调和分析领域，而调和分析的目的是将函数分解成更简单的成分，比如正弦函数。

陶哲轩介绍过：「调和分析作为分析学的重要分支，其核心关注点在于对函数性质的定量刻画。与传统定性研究不同，该领域致力于建立精确的数值界。」

如今，调和分析研究非常活跃，并已成为从数字音视频压缩到电信系统设计等诸多应用中的基础工具。

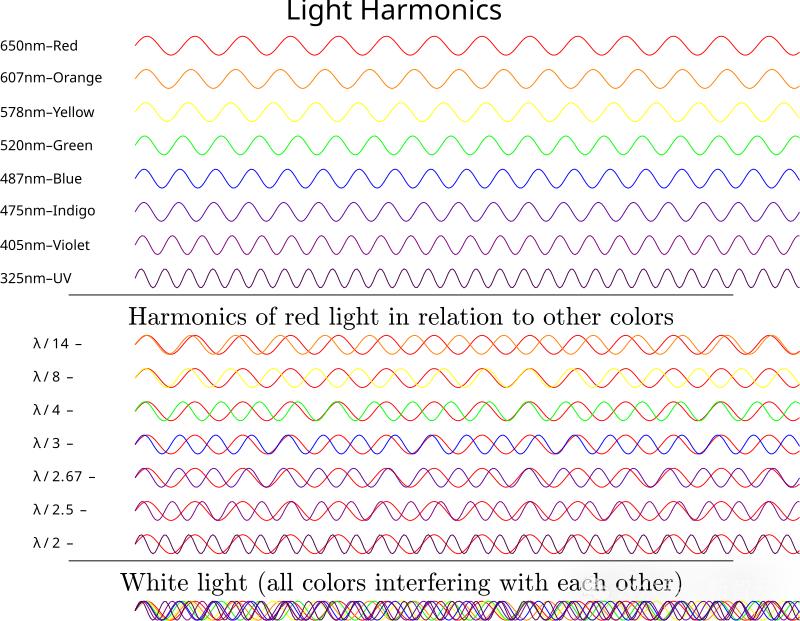
光的调和分析：将白光分解为不同波长的光

调和分析起源于19 世纪初法国数学家约瑟夫·傅里叶（Joseph Fourier）对热方程的研究——一种描述固体中热量扩散的偏微分方程。

约瑟夫·傅里叶：1768年3月21日—1830年5月16日，法国数学家、物理学家，提出傅里叶级数，并将其应用于热传导理论与振动理论。年幼时，父母双亡；1789年，他跟随拿破仑东征

他发明的傅里叶级数 (Fourier series)方法，将复杂函数分解为正弦和余弦的和，为理解物理与数学现象开启了全新视角。

在调和分析理论中，一切都是由波构成的。如果你选对足够多的波，就能「建造」任何东西

在所谓的傅里叶限制性理论 (Fourier restriction theory) 中，研究者关注有限类型的波能构造出什么结构。

限制性猜想（Restriction Conjecture）作为调和分析的核心问题之一，主要研究定义在曲面上的函数的傅里叶变换性质，其核心论断在于：这类傅里叶变换的等高集会保持相对较小的测度。

上世纪80年代，Mizohata-Takeuchi猜想则进一步探究这些等高集的几何形态，特别是它们在何种程度上能够避免沿直线聚集的特性。

Cairo回忆道：「当我得到第一个反例后，我尝试将整个问题转到频域 (frequency space)去重构。我观察到我的构造在频率域中的展现形态。随后我意识到，其实还有一种更简洁的方法来设计反例。」

反例不是质疑，而是数学最锋利的语言。

17岁的她，给出了震惊四座的答案。

在西班牙San José会场，她提出了这番思路。

2025年6月9日至13日，第12届国际调和分析与偏微分方程大会 (International Congress on Harmonic Analysis and Partial Differential Equations)在那里举行。

这是由马德里自治大学下属数学科学研究所 (ICMAT) 主办的El Escorial会议，其近50年的历史中，一直是该领域极具声望的盛会之一

这是Cairo的首次国际科学之行。能与其他同样热爱数学的人相聚，Cairo感到这真是太美好了。

在大会上，她做了会议预定中的报告之一。她没有紧张，反而非常享受这次演讲。

她喜欢讲数学，也不介意「教」年纪比她大的学生。

除了数学，她还有更深的志向：「助人为乐，予人幸福」。

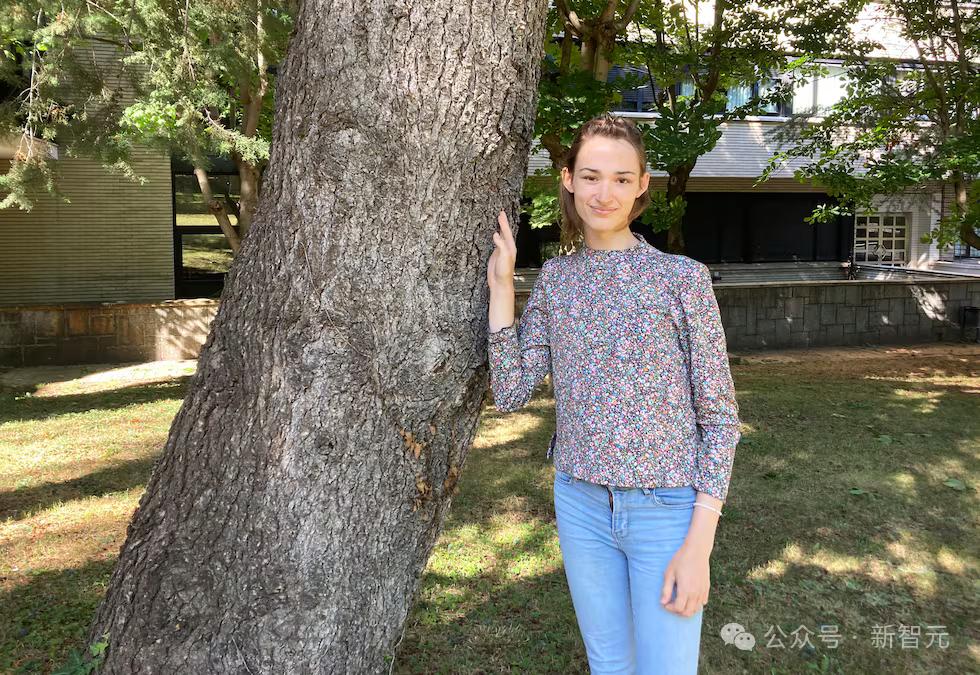
天才少女

早已种下数学梦想，13岁想做数论

从有记忆起，她就对数学怀有浓厚兴趣。

她曾自学高深的数学教材，一直梦想成为数学家。

「我一直梦想成为数学家，但直到我自学抽象代数 (abstract algebra) 后，才真正理解这身份意味着什么。有趣的是，抽象代数和我现在专注的数学方向正好相反。其实，一开始我以为自己会主攻数论 (number theory)。13或14岁时，我甚至撰写了一篇关于数论的论文，但研究的问题似乎没人关心。」

忆及此处，她自己不禁笑出声来。

在新冠疫情期间，Berkeley Math Circle的夏令营转为线上举办。